Question

Practice question — Given the trapezoid to the right find the length of legs in the following isosceles trapezoid

Answer 1

Given:

A figure of an isosceles trapezoid with bases 18 and 24, and the vertical height is 4.

To find:

The legs of the isosceles trapezoid.

Solution:

Draw another perpendicular and name the vertices as shown in the below figure.

From the figure it is clear that the AEFD is a rectangle. So,

`EF=AD=18`

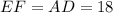
Since ABCD is an isosceles trapezoid, therefore in triangle ABE and DCF,

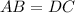`AB=DC` (Legs of isosceles trapezoid)

`AE=DF` (Vertical height of isosceles trapezoid)

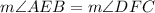`m\angle AEB=m\angle DFC` (Right angle)

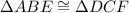`\Delta ABE\cong \Delta DCF` (HL postulate)

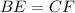`BE=CF` (CPCTC)

Now,

`BE+EF+FC=BC`

`2BE+18=24`

`2BE=24-18`

`2BE=6`

`BE=3`

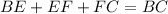
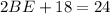
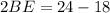
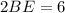
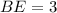
Using Pythagoras theorem in triangle ABE, we get

`Hypotenuse^2=Perpendicular^2+Base^2`

`(AB)^2=(AE)^2+(BE)^2`

`(AB)^2=(4)^2+(3)^2`

`(AB)^2=16+9`

`(AB)^2=25`

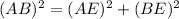
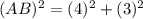
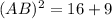
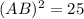
Taking square root on both sides, we get

`AB=\pm √(25)`

`AB=\pm 5`

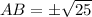
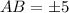
Side length cannot be negative. So,
`AB=5`.

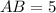Therefore, the length of legs in the given isosceles trapezoid is 5 units.