Given:
A figure of an isosceles trapezoid with bases 18 and 24, and the vertical height is 4.
To find:
The legs of the isosceles trapezoid.
Solution:
Draw another perpendicular and name the vertices as shown in the below figure.
From the figure it is clear that the AEFD is a rectangle. So,
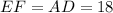
Since ABCD is an isosceles trapezoid, therefore in triangle ABE and DCF,
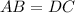 (Legs of isosceles trapezoid)
(Legs of isosceles trapezoid)
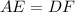 (Vertical height of isosceles trapezoid)
(Vertical height of isosceles trapezoid)
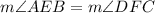 (Right angle)
(Right angle)
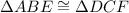 (HL postulate)
(HL postulate)
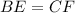 (CPCTC)
(CPCTC)
Now,
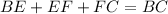
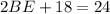
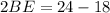
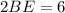
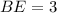
Using Pythagoras theorem in triangle ABE, we get
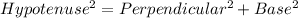
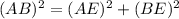
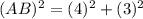
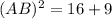
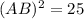
Taking square root on both sides, we get
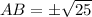
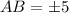
Side length cannot be negative. So,
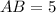 .
.
Therefore, the length of legs in the given isosceles trapezoid is 5 units.