Question

PLS SOMEONE HELP ME QUICKLY

Answer 1

Given:

In a parallelogram
`PRTV, VQ\perp PR,VS\perp RT`.

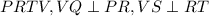To prove:

`(PQ)/(ST)=(PV)/(VT)`

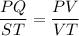
Solution:

It is given that
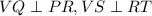`VQ\perp PR,VS\perp RT`, it means
`\angle PQV` and
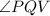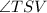`\angle TSV` are right angle triangles.

In triangle PQV and triangle TSV,

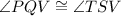`\angle PQV\cong \angle TSV` (Right angles)

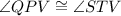`\angle QPV\cong \angle STV` (Opposite angles of a parallelogram)

Two corresponding angles are congruent. So, by AA property of similarity, we get

`\Delta PQV\sim \Delta TSV`

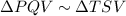
We know that the corresponding parts of similar triangles are proportional. So,

`(PQ)/(TS)=(PV)/(TV)`

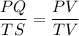
It can be rewritten as:

`(PQ)/(ST)=(PV)/(VT)`

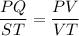
Hence proved.