1 Answer

Starsky · Answer 1 · 2022-09-19T12:50:22+0000

Given:

In a parallelogram
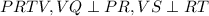$PRTV, VQ\perp PR,VS\perp RT$ .

To prove:

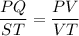
(PQ)/(ST)=(PV)/(VT)

Solution:

It is given that
$VQ\perp PR,VS\perp RT$ , it means
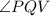$\angle PQV$ and
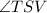$\angle TSV$ are right angle triangles.

In triangle PQV and triangle TSV,

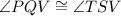$\angle PQV\cong \angle TSV$ (Right angles)

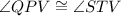$\angle QPV\cong \angle STV$ (Opposite angles of a parallelogram)

Two corresponding angles are congruent. So, by AA property of similarity, we get

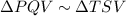
$\Delta PQV\sim \Delta TSV$

We know that the corresponding parts of similar triangles are proportional. So,

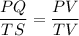
(PQ)/(TS)=(PV)/(TV)

It can be rewritten as:

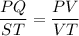
(PQ)/(ST)=(PV)/(VT)

Hence proved.

Please log in or register to add a comment.