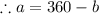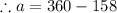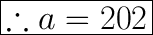1 Answer

Pdu · Answer 1 · 2022-06-23T01:21:20+0000

Answer:

$\huge \orange {\boxed {a =202\degree}}$

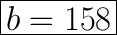
$\huge \purple {\boxed { b = 158\degree}}$

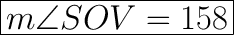
$\huge \red {\boxed {m\angle SOV = 158\degree}}$

Explanation:

In
$\odot$ O, ST and VT are tangents at points S and V respectively.

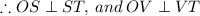
$\therefore OS\perp ST, \:and\: OV\perp VT$

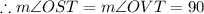
$\therefore m\angle OST=m\angle OVT = 90\degree$

In quadrilateral OSTV,

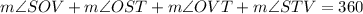
$m\angle SOV +m\angle OST+m\angle OVT+m\angle STV = 360\degree$

(By interior angle sum postulate of a quadrilateral)

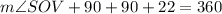
$m\angle SOV +90\degree +90\degree +22\degree = 360\degree$

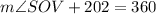
$m\angle SOV +202\degree = 360\degree$

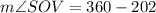
$m\angle SOV = 360\degree-202\degree$

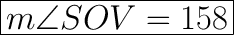
$\huge \red {\boxed {m\angle SOV = 158\degree}}$

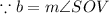
$\because b = m\angle SOV$

(Measure of minor arc is equal to measure of its corresponding central angle)

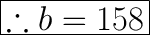
$\huge \purple {\boxed {\therefore b = 158\degree}}$

$\because a + b= 360\degree$

(By arc sum property of a circle)

$\therefore a = 360\degree - b$

$\therefore a = 360\degree -158\degree$

$\huge \orange {\boxed {\therefore a =202\degree}}$

Please log in or register to add a comment.