Question↷
Which statement best reflects the solution(s) of the equation?
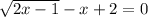
Answer↷
There is only one solution: x = 5 .
The solution x = 1 is an extraneous solution.
Solution↷
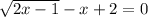
- Taking (-x+2) to the other side
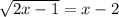
- squaring both of the sides
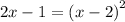
- expanding the sqared binomial as ㅤㅤㅤㅤ(a-b)²= a²- 2ab + b²
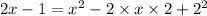
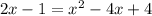
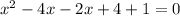

- using splitting middle term method

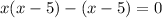

so the root would either be 5 or 1
_____________________________________
putting the value of x as 1,
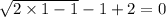
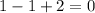
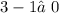
hence , it's not the true solution of the equation
_____________________________________
putting the value of x as 5,
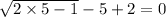
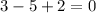


hence ,it's the true solution of the equation