Question

A plane flies against the wind 288 miles from Los Angeles to San Jose and then returns home with the same wind. The wind speed is 60 mph. If the total flying time was 2 hours, what is the speed of the plane?

Answer 1

The speed of the airplane is 300 miles per hour.

Explanation:

Let consider that plane travels at constant speed, which is the sum of the velocity of the plane in still air (velocity of the plane relative to wind) and the velocity of the wind. Hence, the total time spent by the plane is described by following kinematic formula:

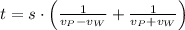`t = s\cdot \left((1)/(v_(P)-v_(W))+(1)/(v_(P)+v_(W)) \right)` (1)

Where:

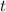`t` - Total time, in hours.

`s` - Distance between Los Angeles and San Jose, in miles.

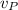`v_(P)` - Velocity of the plane in still air, in miles per hour.

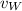`v_(W)` - Velocity of the wind, in miles per hour.

Then, we proceed to simplify the formula and clear the speed of the plane in still air:

`(t)/(s) = (2\cdot v_(P))/(v_(P)^(2)-v_(W)^(2))`

`\left((t)/(s)\right)\cdot (v_(P)^(2)-v_(W)^(2)) = 2\cdot v_(P)`

`\left((t)/(s) \right)\cdot v_(P)^(2) - 2\cdot v_(P)- \left((t)/(s) \right)\cdot v_(W)^(2) = 0`

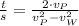
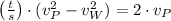
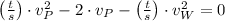
Which is a Second Order Polynomial, whose roots can be found analytically by Quadratic Formula. If we know that
`t = 2\,h`,
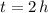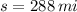`s = 288\,mi` and
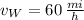`v_(W) = 60\,(mi)/(h)`, then we have the following polynomial:

`(1)/(144)\cdot v_(P)^(2)-2\cdot v_(P) -25 = 0`

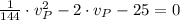
The two roots associated with this polynomial are, respectively:

`v_(P,1) = 300\,(mi)/(h)`,
`v_(P,2) = -12\,(mi)/(h)`

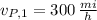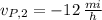
Since speed is the magnitude of velocity, then solution must be positive. First root satisfies all these conditions.

In a nutshell, the speed of the airplane is 300 miles per hour.