Answer:
Ava is incorrect
Explanation:
Given

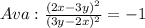
Required
Determine if Ava is correct or not
Ava's solution is incorrect and the proof is as follows;

Apply the following law of indices;
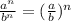
![((2x - 3y)^2)/((3y - 2x)^2) = [(2x - 3y)/(3y - 2x)]^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/7y28akdn4zr4ok2mbzvxgn7ttacz917c7c.png)
Rewrite the numerator
![((2x - 3y)^2)/((3y - 2x)^2) = [(-(3y - 2x))/(3y - 2x)]^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/an5lxzs7snsrclkqiy9tuo46krubzehncy.png)
Cross out the common factor of the numerator and denominator
![((2x - 3y)^2)/((3y - 2x)^2) = [(-1)/(1)]^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/k92tpbjkyvtijr12bldezf1b9gw3dy6lhk.png)
![((2x - 3y)^2)/((3y - 2x)^2) = [-1]^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/i6z4o6t8ga6mom7yt92zhlcew0ysufbv9z.png)
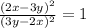
Hence, the solution is 1; not -1
Her mistake is that, she did not apply the square on -1, after she factorize the denominator