Answer:
The ranking of the top three teams could occur in 720 ways.
Explanation:
The order in which the teams are ranked is important, that is, for example, Oilers, Flames and Canucks is a different outcome of Oilers, Canucks and Flames. This means that the permutations formula is used to solve this question.
Permutations formula:
The number of possible permutations of x elements from a set of n elements is given by the following formula:
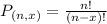
In how many ways could the ranking of the top three teams occur?
Three teams from a set of 10. So
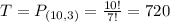
The ranking of the top three teams could occur in 720 ways.