Answer: 1.25
Explanation:
Given: A college-entrance exam is designed so that scores are normally distributed with a mean
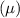 = 500 and a standard deviation
= 500 and a standard deviation
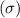 = 100.
= 100.
A z-score measures how many standard deviations a given measurement deviates from the mean.
Let Y be a random variable that denotes the scores in the exam.
Formula for z-score =
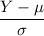
Z-score =
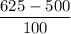
⇒ Z-score =
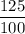
⇒Z-score =1.25
Therefore , the required z-score = 1.25