Options
A. UV = 14 ft and m∠TUV = 45°
B. TU = 26 ft
C. m∠STU = 37° and m∠VTU = 37°
D. ST = 20 ft, UV = 14 ft, and m∠UST = 98°
E. m∠UST = 98° and m ∠TUV = 45°
Answer:
A. UV = 14 ft and m∠TUV = 45°
D. ST = 20 ft, UV = 14 ft, and m∠UST = 98°
Explanation:
Given
See attachment for triangle
Required
What proves that: ΔSTU ≅ ΔVTU using SAS
To prove their similarity, we must check the corresponding sides and angles of both triangles
First:
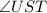 must equal
must equal
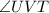
So:
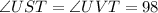
Next:
UV must equal US.
So:
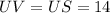
Also:
ST must equal VT
So:
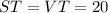
Lastly
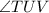 must equal
must equal
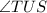
So:
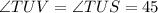
Hence: Options A and D are correct