Question

Identify each expression and value that represents the area under the curve y= x^2+4 on the interval [-3, 2].

Answer 1

The area is given exactly by the definite integral,

`\displaystyle\int_(-3)^2(x^2+4)\,\mathrm dx=\left(\frac{x^3}3+5x\right)\bigg|_(-3)^2=\frac{95}3\approx31.67`

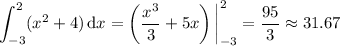
We can write this as a Riemann sum, i.e. the infinite sum of rectangular areas:

• Split up the integration interval into n equally-spaced subintervals, each with length (2 - (-3))/n = 5/n - - this will be the width of each rectangle. The intervals would then be

[-3, -3 + 5/n], [-3 + 5/n, -3 + 10/n], …, [-3 + 5(n - 1)/n, 2]

• Over each subinterval, take the function value at some point x * to be the height.

Then the area is given by

`\displaystyle\lim_(n\to\infty)\sum_(k=1)^nf(x^*)\Delta x_k=\lim_(n\to\infty)\sum_(k=1)^nf(x^*)\frac5n`

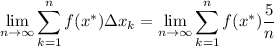
Now, if we take x * to be the left endpoint of each subinterval, we have

x * = -3 + 5(k - 1)/n → f (x *) = (-3 + 5(k - 1)/n)² + 4

If we instead take x * to be the right endpoint, then

x * = -3 + 5k/n → f (x *) = (-3 + 5k/n)² + 4

So as a Riemann sum, the area is represented by

`\displaystyle\lim_(n\to\infty)\sum_(k=1)^n\left(\left(-3+\frac{5k}n\right)^2+4\right)\frac5n`

and if you expand the summand, this is the same as

`\displaystyle\lim_(n\to\infty)\sum_(k=1)^n\left(13-\frac{30k}n+(25k^2)/(n^2)\right)\frac5n=\lim_(n\to\infty)\sum_(k=1)^n\left(\frac{65}n-(150k)/(n^2)+(125k^2)/(n^3)\right)`

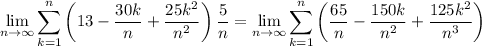
So from the given choices, the correct ones are

• row 1, column 1

• row 2, column 2

• row 4, column 2

Answer 2

Explanation: