The area is given exactly by the definite integral,
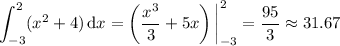
We can write this as a Riemann sum, i.e. the infinite sum of rectangular areas:
• Split up the integration interval into n equally-spaced subintervals, each with length (2 - (-3))/n = 5/n - - this will be the width of each rectangle. The intervals would then be
[-3, -3 + 5/n], [-3 + 5/n, -3 + 10/n], …, [-3 + 5(n - 1)/n, 2]
• Over each subinterval, take the function value at some point x * to be the height.
Then the area is given by
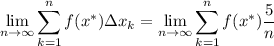
Now, if we take x * to be the left endpoint of each subinterval, we have
x * = -3 + 5(k - 1)/n → f (x *) = (-3 + 5(k - 1)/n)² + 4
If we instead take x * to be the right endpoint, then
x * = -3 + 5k/n → f (x *) = (-3 + 5k/n)² + 4
So as a Riemann sum, the area is represented by
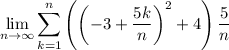
and if you expand the summand, this is the same as
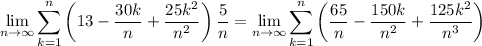
So from the given choices, the correct ones are
• row 1, column 1
• row 2, column 2
• row 4, column 2