Answer:
B
Explanation:
You find the multiplicity by looking at the power of the original root. You can imagine it as
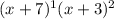 . Now set those equal to 0 to find the value of them as roots.
. Now set those equal to 0 to find the value of them as roots.
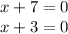
Solve them both and you get:

Now as we saw in the origin of the roots above that (x + 7) was raised to the first power. That means it has a multiplicity of one, which also means it crosses when it reaches the x-axis. (x + 3) however had a multiplicity of 2, since it was squared. That means that (x + 3) will touch and turn the x-axis.
Therefore the answer is B since that agrees with everything we said.