Given:
The function is:
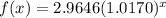
To find:
Rewrite the exponential equation given above using base e.
Solution:
The exponential models is:
 ...(i)
...(i)
Where P is initial values, r is the rate of interest and x is the time period.
The exponential models using base e is:
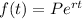 ...(ii)
...(ii)
Where, P is initial values, r is the rate of interest and t is the time period.
The given function is:
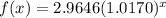
It can be written as:
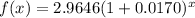 ...(iii)
...(iii)
On comparing (i) and (iii), we get
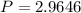
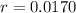
Putting
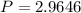 and
and
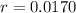 in (ii), we get
in (ii), we get

Therefore, the correct option is D.