Hi there!
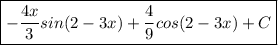
To find the indefinite integral, we must integrate by parts.
Let "u" be the expression most easily differentiated, and "dv" the remaining expression. Take the derivative of "u" and the integral of "dv":
u = 4x
du = 4
dv = cos(2 - 3x)
v = 1/3sin(2 - 3x)
Write into the format:
∫udv = uv - ∫vdu
Thus, utilize the solved for expressions above:
4x · (-1/3sin(2 - 3x)) -∫ 4(1/3sin(2 - 3x))dx
Simplify:
-4x/3 sin(2 - 3x) - ∫ 4/3sin(2 - 3x)dx
Integrate the integral:
∫4/3(sin(2 - 3x)dx
u = 2 - 3x
du = -3dx ⇒ -1/3du = dx
-1/3∫ 4/3(sin(2 - 3x)dx ⇒ -4/9cos(2 - 3x) + C
Combine:
