Answer:
Option (3)
Explanation:
By the theorem, angle between two tangents intersecting each other outside the circle is half of the difference between intercepted arcs.
From the figure attached,
Two tangents CD and DE are intersecting each other at point D outside the circle A.
Two intercepted arcs are minor arc CE and major arc CBE,
Measure of arc CE = 112°
Therefore, measure of major arc CBE = 360° - 112°
= 248°
m(∠CDE) =
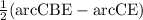
=
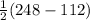
=
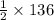
= 68°
Option (3) will be the correct option.