Answer:
![\begin{array}{ccccccccccccccc}{1} & {3} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {57} & {58} & {61} \\ \end{array}]()
Explanation:
Given
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {[ \ ] } & {15} & {18}& {[ \ ] } & {[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {[ \ ]} \\ \end{array}]()
Required
Fill in the box
From the question, the range is:
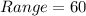
Range is calculated as:
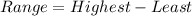
From the box, we have:
So:
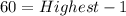
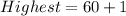
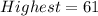
The box, becomes:
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {[ \ ] } & {15} & {18}& {[ \ ] } & {[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
From the question:
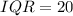--- interquartile range
This is calculated as:
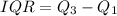
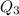is the median of the upper half while
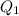is the median of the lower half.
So, we need to split the given boxes into two equal halves (7 each)
Lower half:
![\begin{array}{ccccccc}{1} & {[ \ ]} & {4} & {[ \ ] } & {15} & {18}& {[ \ ] } \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/ze4hq0qam3rp55lqsx8oahkn3tb1b9451l.png)
Upper half
![\begin{array}{ccccccc}{[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/k45gf781hbtztfy7ucy8bjvjui7sls6gw4.png)
The quartile is calculated by calculating the median for each of the above halves is calculated as:
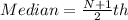
Where N = 7
So, we have:
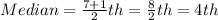
So,
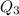= 4th item of the upper halves
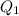= 4th item of the lower halves
From the upper halves
We have:
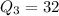
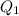can not be determined from the lower halves because the 4th item is missing.
So, we make use of:
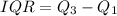
Where
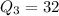and
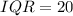
So:
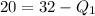
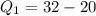
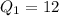
So, the lower half becomes:
Lower half:
![\begin{array}{ccccccc}{1} & {[ \ ]} & {4} & {12 } & {15} & {18}& {[ \ ] } \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/5g51dl7wq5cim772gu73w1dydynix2ddib.png)
From this, the updated values of the box is:
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {12} & {15} & {18}& {[ \ ] } & {[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
From the question, the median is:
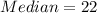and
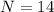
To calculate the median, we make use of:
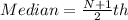
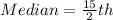
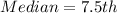
This means that, the median is the average of the 7th and 8th items.
The 7th and 8th items are blanks.
However, from the question; the mode is:
Since the values of the box are in increasing order and the average of 18 and 18 do not equal 22 (i.e. the median), then the 7th item is:
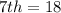
The 8th item is calculated as thus:
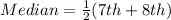
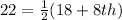
Multiply through by 2
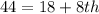
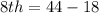
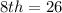
The updated values of the box is:
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
From the question.
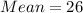
Mean is calculated as:
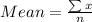
So, we have:
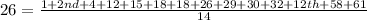
Collect like terms
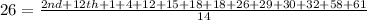
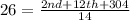
Multiply through by 14
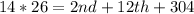
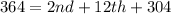
This gives:
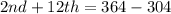
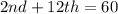
From the updated box,
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
We know that:
The 2nd value can only be either 2 or 3
The 12th value can take any of the range 33 to 57
Of these values, the only possible values of 2nd and 12th that give a sum of 60 are:
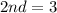
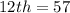
i.e.
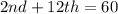
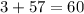
So, the complete box is:
![\begin{array}{ccccccccccccccc}{1} & {3} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {57} & {58} & {61} \\ \end{array}]()