Answer:
![\begin{array}{ccccccccccccccc}{1} & {3} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {57} & {58} & {61} \\ \end{array}]()
Explanation:
Given
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {[ \ ] } & {15} & {18}& {[ \ ] } & {[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {[ \ ]} \\ \end{array}]()
Required
Fill in the box
From the question, the range is:
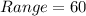
Range is calculated as:
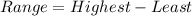
From the box, we have:
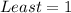
So:
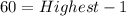
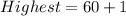
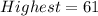
The box, becomes:
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {[ \ ] } & {15} & {18}& {[ \ ] } & {[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
From the question:
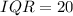 --- interquartile range
--- interquartile range
This is calculated as:
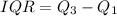
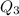 is the median of the upper half while
is the median of the upper half while
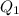 is the median of the lower half.
is the median of the lower half.
So, we need to split the given boxes into two equal halves (7 each)
Lower half:
![\begin{array}{ccccccc}{1} & {[ \ ]} & {4} & {[ \ ] } & {15} & {18}& {[ \ ] } \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/ze4hq0qam3rp55lqsx8oahkn3tb1b9451l.png)
Upper half
![\begin{array}{ccccccc}{[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/k45gf781hbtztfy7ucy8bjvjui7sls6gw4.png)
The quartile is calculated by calculating the median for each of the above halves is calculated as:
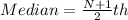
Where N = 7
So, we have:
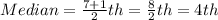
So,
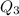 = 4th item of the upper halves
= 4th item of the upper halves
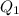 = 4th item of the lower halves
= 4th item of the lower halves
From the upper halves
![\begin{array}{ccccccc}{[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/k45gf781hbtztfy7ucy8bjvjui7sls6gw4.png)
We have:
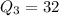
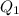 can not be determined from the lower halves because the 4th item is missing.
can not be determined from the lower halves because the 4th item is missing.
So, we make use of:
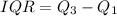
Where
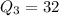 and
and
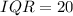
So:
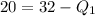
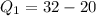
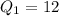
So, the lower half becomes:
Lower half:
![\begin{array}{ccccccc}{1} & {[ \ ]} & {4} & {12 } & {15} & {18}& {[ \ ] } \\ \end{array}](https://img.qammunity.org/2022/formulas/mathematics/college/5g51dl7wq5cim772gu73w1dydynix2ddib.png)
From this, the updated values of the box is:
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {12} & {15} & {18}& {[ \ ] } & {[ \ ]} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
From the question, the median is:
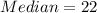 and
and
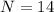
To calculate the median, we make use of:
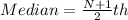
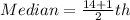
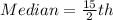
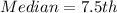
This means that, the median is the average of the 7th and 8th items.
The 7th and 8th items are blanks.
However, from the question; the mode is:
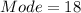
Since the values of the box are in increasing order and the average of 18 and 18 do not equal 22 (i.e. the median), then the 7th item is:
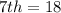
The 8th item is calculated as thus:
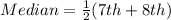
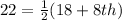
Multiply through by 2
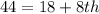
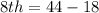
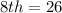
The updated values of the box is:
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
From the question.
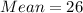
Mean is calculated as:
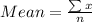
So, we have:
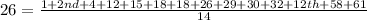
Collect like terms
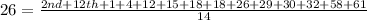
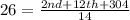
Multiply through by 14
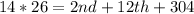
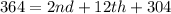
This gives:
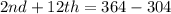
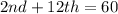
From the updated box,
![\begin{array}{ccccccccccccccc}{1} & {[ \ ]} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {[ \ ]} & {58} & {61} \\ \end{array}]()
We know that:
The 2nd value can only be either 2 or 3
The 12th value can take any of the range 33 to 57
Of these values, the only possible values of 2nd and 12th that give a sum of 60 are:
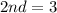
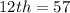
i.e.
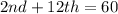
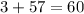
So, the complete box is:
![\begin{array}{ccccccccccccccc}{1} & {3} & {4} & {12} & {15} & {18}& {18 } & {26} & {29} & {30} & {32} & {57} & {58} & {61} \\ \end{array}]()