Question

g A thin-walled pressure vessel 6-cm thick originally contained a small semicircular flaw (radius 0.50-cm) located at the inner surface and oriented normal to the hoop stress direction. Repeated pressure cycling enabled the crack to grow larger. If the fracture toughness of the material is , the yield strength equal to 1250 MPa, and the hoop stress equal to 300 MPa, would the vessel leak before it ruptured

Answer 1

This question is not complete, the complete question is;

A thin-walled pressure vessel 6-cm thick originally contained a small semicircular flaw (radius 0.50-cm) located at the inner surface and oriented normal to the hoop stress direction. Repeated pressure cycling enabled the crack to grow larger. If the fracture toughness of the material is
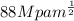`88 Mpam^(1)/(2)` , the yield strength equal to 1250 MPa, and the hoop stress equal to 300 MPa, would the vessel leak before it ruptured

Answer:

length of crack is 5.585 cm

we will observe that, the length of crack (5.585 cm) is less than the vessel thickness (6 cm) Hence, vessel will not leak before it ruptures

Step-by-step explanation:

Given the data in the question;

vessel thickness = 6 cm

fracture toughness k =
`88 Mpam^(1)/(2)`

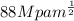
yield strength = 1250 MPa

hoop stress equal = 300 MPa

we know that, the relation between fracture toughness and crack length is expressed as;

k = (1.1)(2/π)(r√(πa))

where k is the fracture toughness, r is hoop stress and a is length of crack

so we rearrange to find length of crack

a = 1/π[( k / 1.1(r)(2/π)]²

a = 1/π[( kπ / 1.1(r)(2)]²

so we substitute

a = 1/π [( 88π / 1.1(300)(2/π)]²

a = 1/π[ 0.1754596 ]

a = 0.05585 m

a = 0.05585 × 100 cm

a = 5.585 cm

so, length of crack is 5.585 cm

we will observe that, the length of crack (5.585 cm) is less than the vessel thickness (6 cm) Hence, vessel will not leak before it ruptures