Question

Please use the following scenario for this question and the following 4 questions. The national academy of sciences reported in a 1997 study that 40% of research in mathematics is published by US authors. The math chairperson of a university wishes to test the claim that this percentage is no longer 40%. He has no indication of whether the percentage has increased or decreased since that time. He surveys a simple random sample of 130 recent articles published by reputable math research journals and finds that 62 of these articles have US authors. Does this evidence support the math chairperson's claim that the percentage is no longer 40%

Answer 1

The evidence does not support the math chairperson's claim that the percentage is no longer 40%

Explanation:

The known population percentage of research in mathematics published by US authors = 40%

The proportion, p = 0.40

Therefore, q = 1 - p = 1 - 0.4 = 0.6

The number of articles in the sample = 130

The number of articles by US authors in the sample = 62

Therefore, the proportion of US authors in the sample,
`\hat p` = (62/130) × 100 =

`0.4\overline{769230}`

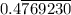
∴ The percentage of US authors in the sample ≈ 47.7%

The null hypothesis, H₀; p = 0.4

The alternative hypothesis, Hₐ; p ≠ 0.4

The z-test is given as follows;

`z=\frac{\hat{p}-p}{\sqrt{(p\cdot q)/(n)}}`

`z=\frac{0.477-0.40}{\sqrt{(0.4* 0.6)/(130)}} \approx 1.792`

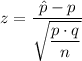
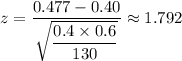
The p-value P(Z > 1.79) = 2 × (1 - 0.96327) = 0.07346

Therefore, given that the p-value is larger than 0.05 there is significant evidence in favor of the null hypothesis and we reject the alternative hypothesis

Therefore, also, there is not enough statistical evidence to support the math chairperson's claim that the percentage is no longer 40%.