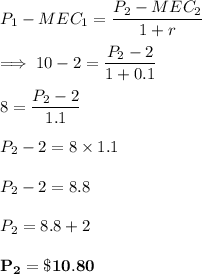Question

Consider a two-period resource allocation problem where the efficient allocation of the resource implies a market price of $10 in the first period. Assume in both periods the constant marginal extraction costs equal $2 and the social discount rate is 10%. The socially efficient undiscounted market price in the second period must be:

Answer 1

$10.80

Step-by-step explanation:

Given that:

A first-period efficient allocation cost = $10

The constant marginal extraction cost MEC for both periods = $2

The social discount rate (r) = 10%

∴

The efficient undiscounted market price for the 2nd period can be determined by using the formula:

`P_1 - MEC_1 = (P_2 -MEC_2)/(1+r) \\ \\ \implies 10 -2 = (P_2-2)/(1+0.1) \\ \\ 8 = (P_2-2)/(1.1) \\ \\ P_2 -2 = 8 * 1.1 \\ \\ P_2-2=8.8 \\ \\ P_2 = 8.8+2 \\ \\ \mathbf{P_2 = \$10.80}`