Answer:
The amount more in interest she will pay if she choose 8 years instead of 5 years loan is approximately $2,665.92
Explanation:
The total worth of debt Crystal has. P = $23,000
The options on the number of years for which the loans for consolidation are available, t = 5 and 8 years
n = 12 × t = The number of monthly payment = 12×5 = 60 or 12 × 8 = 96
The annual percentage rate of the loans, r = 6.75% = 0.0675
The monthly payments, 'M', Crystal pays is given as follows;
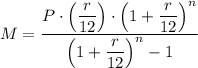
When n = 60, we get;

The total amount payed, A = M × n
∴ The total amount payed when n = 60 is, A₅ = 452.72 × 60 = 27163.2
A₅ ≈ $ 27,163.2
The interest on the loan, I₅ = A₅ - P
∴ I₅ = $27,163.2 - $23,000 = $4,163.2
When n = 80, we get;
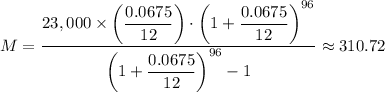
∴ The total amount payed when n = 80 is, A₈ = 310.72 × 96 = 29,829.12
A₈ = $ 29,829.12
The interest on the loan, I₈ = A₈ - P
∴ The interest on the loan, I₈ = 29,829.12 - 23,000 = 6,829.12
The interest Crystal pays when takes the loan for 8 years, I₈ = $6,829.12
Therefore, the amount more interest she will pay if she choose 8 years instead of 5 years loan, ΔI = I₈ - I₅
ΔI = $6,829.12 - $4,163.2 = $2,665.92
The amount more interest she pays if she choose 8 years instead of 5 years loan, ΔI = $2,665.92.