This question is incomplete, the complete question is;
An article in Knee Surgery, Sports Traumatology, Arthroscopy (2005, Vol. 13, pp. 273-279), considered arthroscopic meniscal repair with an absorbable screw. Results showed that for tears greater than 25 millimeters, 13 of 19 repairs were successful while for shorter tears, 22 of 30 repairs were successful.
a) Is there evidence that the success rate is greater for longer tears? Use alpha=0.05
Answer:
P-value = 0.6443
Now, since the p-value( 0.6443 ) is greater than the significance level (0.05), We fail to reject null hypothesis.
Therefore, there is no significant difference in the successive proportion ( rate ).
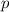₁ =
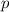₂
Explanation:
Given the data in the question;
Sample of tears greater than 25;
number of successive repairs X₁ = 13
number of repair n₁ = 19
proportion of successive repairs
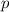₁ = 13/19 = 0.68
q₁ = 1 -
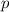₁ = 1 - 0.68 = 0.32
Sample of tears shorter than 25;
number of successive repairs X₂ = 22
number of repair n₂ = 30
proportion of successive repairs
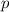₂ = 22/30 = 0.73
q₂ = 1 -
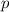₂ = 1 - 0.73 = 0.27
so;
H₀ : There is no significant difference in the successive proportions;
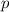₁ =
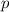₂
Hₐ : The successive rate is greater for longer tears
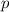₁ >
Significance level ∝ = 0.05
Test Statistics
Z = (
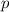₁ -
so we substitute
Z = ( 0.68 - 0.73 / √[ (0.68 ×0.32 / 19) + ( 0.73×0.27 / 30 ) ]
Z = -0.05 / √[ 0.01802 ]
Z = -0.05 / 0.1342
Z = -0.37
P-value for the given test, p = P( Z > -0.37 )
= 1 - P( Z ≤ - 0.37 )
= 1 - 0.35569
P-value = 0.6443
Now, since the p-value( 0.6443 ) is greater than the significance level (0.05), We fail to reject null hypothesis.
Therefore, there is no significant difference in the successive proportion ( rate ).
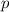₁ =
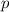₂