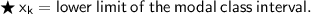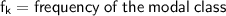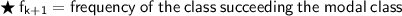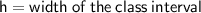Answer:
The class 35 - 40 has maximum frequency. So, it is the modal class.
From the given data,
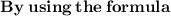
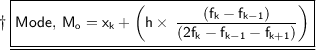
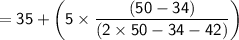
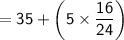
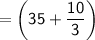
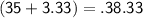

MODE
- Most precisely, mode is that value of the variable at which the concentration of the data is maximum.
MODAL CLASS
- In a frequency distribution the class having maximum frequency is called the modal class.
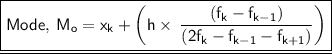
Where,