Answer:
69 degrees
Explanation:
1) Find x
The angles measured x degrees and (x-28) degrees have a sum of 180 degrees because straight lines always have a measure of 180 degrees. Knowing this, construct the equation:

Add 28 to both sides
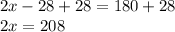
Divide both sides by 2
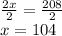
Therefore, x is equal to 104 degrees.
2) Find the measure of the (x-28) degree angle
Plug x into x-28
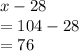
Therefore, the measure of this angle is 76 degrees.
3) Find y
All the interior angles in any triangle will add up to 180 degrees. Knowing this, we can construct another equation:
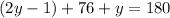
Open up the parentheses

Subtract both sides by 75
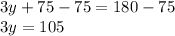
Divide both sides by 3

Therefore, y is equal to 35 degrees.
4) Find the measure of the (2y-1) degree angle
Plug y into 2y-1
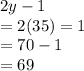
Therefore, y is equal to 69 degrees.
I hope this helps!