Answer:
It's a rectangle, but not a rhombus (or square).
Explanation:
Let's see the vectors of each next vertex:
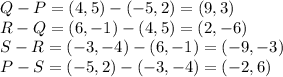
Firstly, we can notice that it's a parallelogram - because the Q-P side is parallel to the S - R side (if the x:y ratios are the same, the sides are parallel).
A rhombus needs the sides to be of the same length. But the length of a (x, y) vector is
 and
and
 , we don't even have to compute it exactly. If it's not a rhombus, it's also not a square (every square is a rhombus).
, we don't even have to compute it exactly. If it's not a rhombus, it's also not a square (every square is a rhombus).
The last thing left is to know if it's a rectangle - for it to be a rectangle, we need to check if the vectors are perpendicular.
We can compute the dot product of the vectors - perpendicular vectors always have a dot product equal to zero. The dot product of two vectors
 and
and
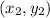 is equal to
is equal to
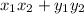 .
.
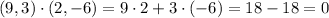
So the sides are perpendicular, and as such - the figure is a rectangle.