Question

Find the other endpoint of the line segment with the given endpoint and midpoint

Endpoint: (3,5)
Midpoint: (7, -2)

Answer 1

The other endpoint is (11,-9)

Explanation:

Midpoint Formula

`\large\boxed{((x_1+x_2)/(2),(y_1+y_2)/(2) )}`

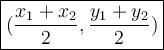
We already know the another endpoint which is (3,5). We substitute x = 3 and y = 5 in the formula. You can substitute in x1, x2 or y1, y2. I'll substitute in first x-term and first y-term instead.

`\large{\begin{cases} (3+x)/(2)=7\\(5+y)/(2)=-2 \end{cases}}`

Because sum of two x-coordinate (along with y-coordinate) divided by two must equal to the midpoint (Let's say that you get the value of midpoint when using midpoint formula.)

Solve the equation for both terms.

`\large{\begin{cases} (3+x)/(2)=7\\(5+y)/(2)=-2 \end{cases}}`

Cancel the denominator by multiplying the whole equation by 2.

`\large{\begin{cases} (3+x)/(2)(2)=7(2)\\(5+y)/(2)(2)=-2(2) \end{cases}}\\\large{\begin{cases} 3+x=14\\ 5+y=-4 \end{cases}}`

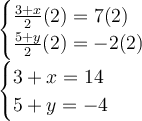
Isolate x-term and y-term.

`\end{cases}}\\\large{\begin{cases} 3+x=14\\ 5+y=-4 \end{cases}}\\\end{cases}}\\\large{\begin{cases} x=14-3\\ y=-4-5 \end{cases}}\\\end{cases}}\\\large{\begin{cases} x=11\\ y=-9 \end{cases}}`

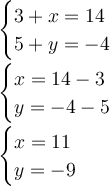
Therefore, when x = 11, y = -9. We can write in ordered pair as (11,-9). The ordered pair (11,-9) is our other endpoint of the line segment. This can be proved by using the distance formula between midpoint and endpoints.

Note: The distance of (3,5) and (7,-2) must equal to the distance of (11,-9) and (7,-2)