Answer:
T₂ = 16.83°C
Step-by-step explanation:
Applying the law of conservation of energy principle here in this situation we get the following equation:
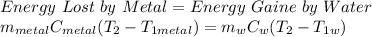
where,
T₂ = Final Temperature of Water = Final Temperature of Metal = ?
C_metal = Specififc Heat Capacity of the metal = 2.11 x 10² J/lg.°C
T_1metal = Initial Temperature of Metal = 225°C
m_metal = mass of metal = 1 x 10⁻²
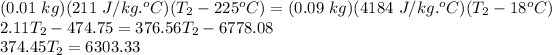 kg (exponent assumed due to missing info in question)
kg (exponent assumed due to missing info in question)
C_w = Specififc Heat Capacity of the water = 4184 J/lg.°C
T_1w = Initial Temperature of water = 18°C
m_w = mass of water = 0.09 kg
Therefore,

T₂ = 16.83°C