Answer:
greater speed will be obtained for the elastic collision,
Step-by-step explanation:
To answer this exercise we must find the speed that the sail acquires after each impact.
Let's start by hitting a ball of clay.
The system is formed by the candle and the clay balls, therefore the forces during the collision are internal and the moment is conserved.
initial instant. before the crash
p₀ = m v₀
where m is the mass of the ball and vo its initial velocity, we are assuming that the candle is at rest
final instant. After the crash
the mass of the candle is M
p_f = (m + M) v
the moment is preserved
p₀ = p_f
m v₀ = (m + M) v
v =
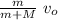
for when n balls have collided
v =
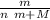 v₀
v₀
Now let's analyze the case of the bouncing ball (elastic)
initial instant
p₀ = m v₀
final moment
p_f = m v_{1f} + M v_{2f}
p₀ = p_f
m v₀ = m v_{1f} + M v_{2f}
m (v₀ - v_{1f}) = M v_{2f}
this case corresponds to an elastic collision whereby the kinetic energy is conserved
K₀ = K_f
½ m v₀² = ½ m v_{1f}² + ½ M v_{2f}²
v₁ = v_{1f} v₂ = v_{2f}
m (v₀² - v₁²) = M v₂²
let's use the identity
(a² - b²) = (a + b) (a-b)
we write our equations
m (v₀ - v₁) = M v₂ (1)
m (v₀ - v₁) (v₀ + v₁) = M v₂²
let's divide these equations
v₀ + v₁ = v₂
Let's look for the final speeds
we substitute in equation 1
m (v₀ - v₁) = M (v₀ + v₁)
v₀ (m -M) = (m + M) v₁
v₁ =
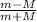 v₀
v₀
we substitute in equation 1 to find v₂
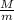 v₂ = v₀ -
v₂ = v₀ -
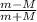 v₀
v₀
v₂ =
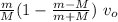
v₂ =
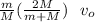
v₂ =
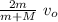
Let's analyze the results for inelastic collision with each ball that collides with the sail, the total mass becomes larger so the speed increase is smaller and smaller.
In the case of elastic collision, the increase in speed is constant with each ball since the total mass remains invariant.
Consequently, greater speed will be obtained for the elastic collision, that is, the ball will bounce.