Answer:
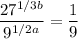
Explanation:
We are given that a and b are positive integers such that:
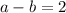
And we want to evaluate:
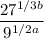
First, note that 27 = 3³ and that 9 = 3². Therefore:
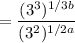
Simplify:
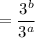
Using the quotient property of exponents:
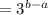
From our given equation, we can divide both sides by -1 to acquire:
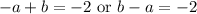
Therefore:
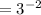
Hence, our answer is:
