Question

Find the area of the largest square contained by a circle of radius r = 1cm. Explain your answer and justify that it is correct. Hint: Use the pythagorean theorem.

Answer 1

2 square cm

Explanation:

Given :

A square is inscribed in a circle whose radius is r = 1 cm

Therefore, the diameter of the circle is 2 r = 2 x 1

= 2 cm.

So the diagonal of the square is 2r.

Using the Pythagoras theorem, we find each of the side of the triangle is
`$r \sqrt 2$`.

Therefore, the area of the square is given by
`$\text{(side)}^2$`

=
`$(r\sqrt 2)^2$`

`$= 2 r^2$`

`$= 2 (1)^2$`

`$=2 \ cm^2$`

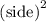
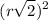
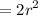
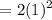
Hence the area of the largest square that is contained by a circle of radius 1 cm is 2 cm square.