Answer:
2 square cm
Explanation:
Given :
A square is inscribed in a circle whose radius is r = 1 cm
Therefore, the diameter of the circle is 2 r = 2 x 1
= 2 cm.
So the diagonal of the square is 2r.
Using the Pythagoras theorem, we find each of the side of the triangle is
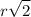 .
.
Therefore, the area of the square is given by
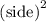
=
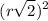
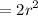
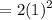
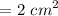
Hence the area of the largest square that is contained by a circle of radius 1 cm is 2 cm square.