Answer:

Explanation:
The probability of matching the number drawn on the gold ball is
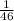
The number of possible pairs of numbers from 1 to 53 is

Choosing 5 numbers, you are choosing 10 different pairs:
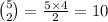
Therefore the probability of correctly matching the drawn pair is
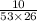
Thus, the probability of winning (matching the pair AND the gold ball) is
