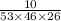Question

In a​ lottery, the top cash prize was ​$642 ​million, going to three lucky winners. Players pick five different numbers from 1 to 53 and one number from 1 to 46. A player wins a minimum award of $400 by correctly matching two numbers drawn from the white balls​ (1 through 53​) and matching the number on the gold ball​ (1 through 46​). What is the probability of winning the minimum​ award?

Answer 1

`(10)/(53 * 46 * 26)`

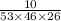
Explanation:

The probability of matching the number drawn on the gold ball is

`(1)/(46)`

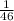
The number of possible pairs of numbers from 1 to 53 is

`\binom{53}{2} = (53 * 52)/(2) = 53 * 26`

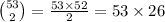
Choosing 5 numbers, you are choosing 10 different pairs:

`\binom{5}{2} = (5 * 4)/(2) = 10`

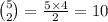
Therefore the probability of correctly matching the drawn pair is

`(10)/(53 * 26)`

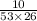
Thus, the probability of winning (matching the pair AND the gold ball) is

`(10)/(53 * 46 * 26)`