Question

A recent article in Business Week listed the "Best Small Companies." We are interested in the current results of the companies' sales and earnings. A random sample of 8 companies was selected and the sales and earnings, in millions of dollars, are reported below. Sales ($million) 89.2 18.6 18.2 71.7 58.6 46.8 17.5 11.9 Earnings ($million) 4.9 4.4 1.3 8 6.6 4.1 2.6 1.7 Let sales be the independent variable and earnings be the dependent variable. (i) Determine the estimated regression equation and comment on the coefficient of X. (ii) For a small company with $50.0 million in sales, estimate the earnings. (iii) Calculate the standard error of estimate and comment on it. (iv) Find the coefficient of determination and interpret the result.

Answer 1

(i) The estimated regression equation is;

`\hat y` ≈ 1.6896 + 0.0604·X

The coefficient of 'X' indicates that
`\hat y` increase by a multiple of 0.0604 for each million dollar increase in sales, X

(ii) The estimated earnings for the company is approximately $4.7096 million

(iii) The standard error of estimate is approximately 29.34

The high standard error of estimate indicates that individual mean do not accurately represent the population mean

(iv) The coefficient of determination is approximately 0.57925

The coefficient of determination indicates that the probability of the coordinate of a new point of data to be located on the line is 0.57925

Explanation:

The given data is presented as follows;

`\begin{array}{ccc}Sales \ (\$million)&&Earning \ (\$million) \\89.2&&4.9\\18.6&&4.4\\18.2&&1.3\\71.7&&8\\58.6&&6.6\\46.8&&4.1\\17.5&&2.6\\11.9&&1.7\end{array}`

(i) From the data, we have;

The regression equation can be presented as follows;

`\hat y` = b₀ + b₁·x

Where;

b₁ = The slope given as follows;

`b_1 = (\Sigma(x_i - \overline x) \cdot (y_i - \overline y))/(\Sigma(x_i - \overline x)^2)`

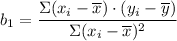
b₀ =
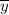`\overline y` - b₁·
`\overline x`

From the data, we have;

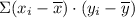`{\Sigma(x_i - \overline x) \cdot (y_i - \overline y)}` = 364.05

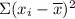`\Sigma(x_i - \overline x)^2}` = 6,027.259

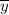`\overline y` = 4.2

`\overline x` = 41.5625

∴ b₁ = 364.05/6,027.259 ≈ 0.06040059005

b₀ = 4.2 - 0.06040059005 × 41.5625 ≈ 1.68960047605 ≈ 1.69

Therefore, we have the regression equation as follows;

`\hat y` ≈ 1.6896 + 0.0604·X

The coefficient of 'X' indicates that the earnings increase by a multiple of 0.0604 for each million dollar increase in sales

(ii) For the small company, we have;

X = $50.0 million, therefore, we get;

`\hat y` = 1.6896 + 0.0604 × 50 = 4.7096

The estimated earnings for the company,
`\hat y` = 4.7096 million

(iii) The standard error of estimate, σ, is given by the following formula;

`\sigma =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(n - 1)}`

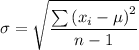
Where;

n = The sample size

Therefore, we have;

`\sigma =\sqrt{(6,027.259 )/(8 - 1)} \approx 29.34`

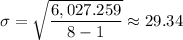
The standard error of estimate, σ ≈ 29.34

The high standard error of estimate indicates that it is very unlikely that a given mean value within the data is a representation of the true population mean

(iv) The coefficient of determination (R Square) is given as follows;

`R^2 = (SSR)/(SST)`

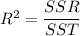
Where;

SSR = The Sum of Squared Regression ≈ 21.9884

SST = The total variation in the sample ≈ 37.96

Therefore, R² ≈ 21.9884/37.96 ≈ 0.57925

The coefficient of determination, R² ≈ 0.57925.

Therefore, by the coefficient of determination, the likelihood of a new introduced data point to located on the line is 0.57925