Answer:
The domain of a function is the set of all possible x values that satisfy the equation. We cannot answer this question without first knowing what the equation for f(x) is.
Explanation:
Take for example the function y = f(x) =
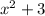 . Here, you can plug in literally any value for x and still get our a real number. Thus, the domain of f(x) is (-∞, ∞).
. Here, you can plug in literally any value for x and still get our a real number. Thus, the domain of f(x) is (-∞, ∞).
However, if your function is y = f(x) =
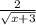 , not every x value is acceptable. First, we cannot have the denominator (bottom part) of the fraction be zero, because division by zero is undefined. Thus, x = -3 is not an acceptable value for x.
, not every x value is acceptable. First, we cannot have the denominator (bottom part) of the fraction be zero, because division by zero is undefined. Thus, x = -3 is not an acceptable value for x.
We also cannot take the square root of a negative number. Thus, we have the rule that x + 3 must be greater than or equal to zero.
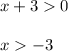
Normally we would use greater than or equal to zero, but because this is in the denominator, we don't want it to equal zero (and thus x = -3 is not acceptable).
So, the domain of x is (-3, ∞). The parenthesis tell us we do not include the negative three and we do not include infinity. In other words, the domain of x is all numbers greater than -3 but less than infinity.
So, first look at your equation for f(x), then see which values of x don't break the rules of math like division by zero or square roots of negative numbers. Good luck!