Given:
Focus of a parabola =
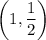
Directrix:
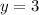
To find:
The equation of the parabola.
Solution:
The equation of a vertical parabola is:
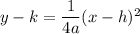 ...(A)
...(A)
Where,
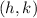 is center,
is center,
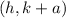 is focus and
is focus and
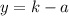 is the directrix.
is the directrix.
On comparing the focus, we get
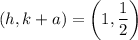
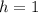
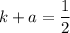 ...(i)
...(i)
On comparing the directrix, we get
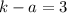 ...(ii)
...(ii)
Adding (i) and (ii), we get
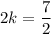
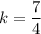
Putting
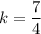 is (i), we get
is (i), we get
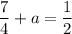
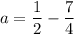
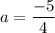
Putting
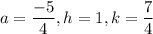 in (A), we get
in (A), we get
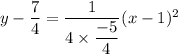
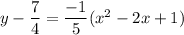
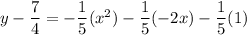
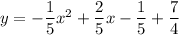
On further simplification, we get
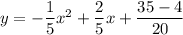
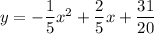
Therefore, the equation of the parabola is
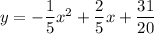 .
.
Note: Option C is correct but the leading coefficient should be negative.