Given:
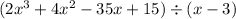
To find:
The quotient by using the synthetic division.
Solution:
We have,
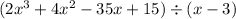
Here,
Dividend =
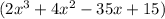
Divisor =
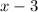
The coefficient of dividend are
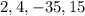 . Write the coefficients of the dividend on the top row and we need to use 3 as divisor for synthetic division. The synthetic division is show below:
. Write the coefficients of the dividend on the top row and we need to use 3 as divisor for synthetic division. The synthetic division is show below:
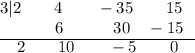
The bottom row represents the coefficients of quotient but the last element of bottom row is the remainder.
Degree of dividend is 3 and degree of division is 1. So, the degree of quotient must be
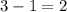 .
.
The quotient is
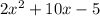 and the reminder is 0.
and the reminder is 0.
Therefore, the correct option is D.