Question

Use synthetic division to solve (2x3+4x2 – 35x+15) +(x-3). What is the quotient?

O 2x2–2x-29+
102
X+ 3
102
O 2x2 - 2x-29+
X-3
2x + 10x2 - 6x
2x2 + 10x-5

Answer 1

Answer: divisor: x+4, dividend: 2x^3+11x^2+18x+9, quotient: 2x^2+5x+3

Explanation:

Answer 2

Given:

`(2x^3+4x^2-35x+15)/ (x-3)`

To find:

The quotient by using the synthetic division.

Solution:

We have,

`(2x^3+4x^2-35x+15)/ (x-3)`

Here,

Dividend =
`(2x^3+4x^2-35x+15)`

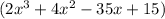
Divisor =
`x-3`

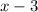
The coefficient of dividend are
`2, 4, -35, 15`. Write the coefficients of the dividend on the top row and we need to use 3 as divisor for synthetic division. The synthetic division is show below:

`3 | 2\quad \quad 4\quad \quad -35\quad \quad 15\\\quad{}\quad{} \quad \quad \ 6\quad \quad \ \ \ 30\quad -15\\\overline{\quad 2\quad \quad 10\quad \quad -5\quad \quad 0\ \ \ }`

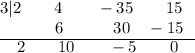
The bottom row represents the coefficients of quotient but the last element of bottom row is the remainder.

Degree of dividend is 3 and degree of division is 1. So, the degree of quotient must be
`3-1=2`.

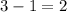The quotient is
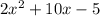`2x^2+10x-5` and the reminder is 0.

Therefore, the correct option is D.