Question

Dwayne drove 18 miles to the airport to pick up his father and then returned home. On the return trip he was able to drive an average of 15 miles per hour faster than he did on the trip there. If the total driving time was 1 hour, then what was his average speed driving to the airport?

Someone please help

Answer 1

Let s represent the speed on the return trip

So, The initial speed will be (s-15)

Equation of time:

`\boxed{ \tt \: time = (distance)/(speed) }`

return time + initial time = 1 hr

`\sf(18)/(s) + (18)/(s - 15) = 1`

⚘Solution for the complete equation in attachment!!~

`\rule{300pt}{2pt}`

• His average speed is 30 km/hr...~

Answer 2

30 mph

Explanation:

Let d = distance (in miles)

Let t = time (in hours)

Let v = average speed driving to the airport (in mph)

⇒ v + 15 = average speed driving from the airport (in mph)

Using: distance = speed x time

`\implies t=(d)/(v)`

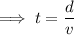
Create two equations for the journey to and from the airport, given that the distance one way is 18 miles:

`\implies t=(18)/(v) \ \ \textsf{and} \ \ t=(18)/(v+15)`

We are told that the total driving time is 1 hour, so the sum of these expressions equals 1 hour:

`\implies (18)/(v) +(18)/(v+15)=1`

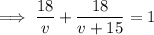
Now all we have to do is solve the equation for v:

`\implies (18(v+15))/(v(v+15)) +(18v)/(v(v+15))=1`

`\implies (18(v+15)+18v)/(v(v+15))=1`

`\implies 18(v+15)+18v=v(v+15)`

`\implies 18v+270+18v=v^2+15v`

`\implies v^2-21v-270=0`

`\implies (v-30)(v+9)=0`

`\implies v=30, v=-9`

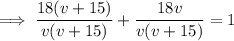
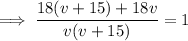
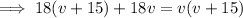
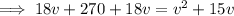
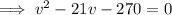
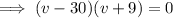
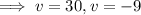
As v is positive, v = 30 only

So the average speed driving to the airport was 30 mph

(and the average speed driving from the airport was 45 mph)