Answer:
30 mph
Explanation:
Let d = distance (in miles)
Let t = time (in hours)
Let v = average speed driving to the airport (in mph)
⇒ v + 15 = average speed driving from the airport (in mph)
Using: distance = speed x time
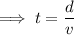
Create two equations for the journey to and from the airport, given that the distance one way is 18 miles:

We are told that the total driving time is 1 hour, so the sum of these expressions equals 1 hour:
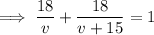
Now all we have to do is solve the equation for v:
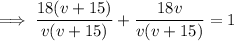
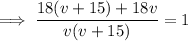
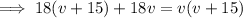
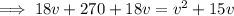

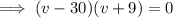
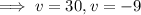
As v is positive, v = 30 only
So the average speed driving to the airport was 30 mph
(and the average speed driving from the airport was 45 mph)