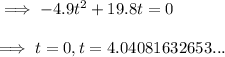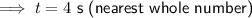Answer:
1) 58 m
2) t = 2 s
3) 78 m
4) t = 6 s
5) It changes the y-intercept (58) to zero
6)
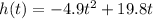
7) h = 20 m
t = 4 s
Explanation:
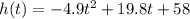
1) When t = 0:
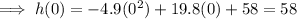
Therefore, the height of the cannon before it is launched is 58 m
2) To find the time when the parabola reaches its max height, differentiate the function with respect to t, equal to zero, then solve for t:
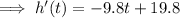
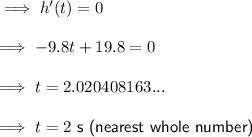
3) The maximum height of the cannonball is when t = 2.020408163...:
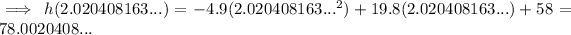
Therefore, the maximum height of the cannonball is 78 m (nearest whole number)
4) Set the function to zero and solve for t:

As time is positive, t = 6 s (nearest whole number)
5) If you launch the cannonball from the ground, where
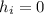 , then the y-intercept will be 0 and the function will be
, then the y-intercept will be 0 and the function will be
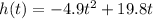
6)
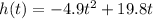
7) To find the maximum height of the parabola, differentiate the function with respect to t, equal to zero, solve for t, then substitute the found value for t into the equation:
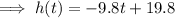
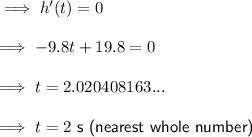
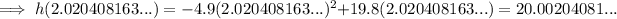

To find the time it took to hit the ground, set the function to zero and solve for t: