Answer:
A
Explanation:
We want to solve the equation:
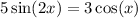
To do so, we can rewrite the equation.
Recall the double-angle identity for sine:
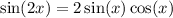
By substitution:
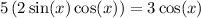
Distribute:
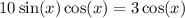
We can subtract 3cos(x) from both sides:
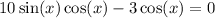
And factor:
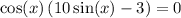
Hence, our answer is A.
*It is important to note that we should not divide both sides by cos(x) to acquire 10sin(x) = 3. This is because we need to find the values of x, and one or more may result in cos(x) = 0 and we cannot divide by 0. Hence, we should subtract and then factor.