Answer:
t = 9.52 s
Step-by-step explanation:
This is an oscillatory motion exercise, in which the angular velocity is
w =
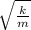
Let's use hooke's law to find the spring constant, let's write the equilibrium equation
F_e - W = 0
F_e = W
k x = m g
k =
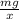
k = 0.545 9.8 /0.0356
k = 150 N / m
now the angular velocity is related to the period
W = 2π / T
we substitute
4π² T² = k /m
T = 4pi²
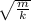
we substitute
T = 4 pi²
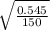
T = 2.38 s
therefore for the spring to oscillate 4 complete periods the time is
t = 4 T
t = 4 2.38
t = 9.52 s