Question

Please help The position of masses 4kg, 6kg, 7kg, 10kg, 2kg, and 12kg are (-1,1), (4,2), (-3,-2), (5,-4), (-2,4) and (3,-5) respectively. Determine the position of the center of mass of this system?​

Answer 1

(1.9756, -2.1951)

Step-by-step explanation:

The center of mass equation is:
`x_(cm)` =
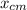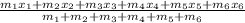`(m_(1)x_(1) + m_(2)x_(2) + m_(3)x_(3) + m_(4)x_(4) + m_(5)x_(5) + m_(6)x_(6))/(m_(1) + m_(2) + m_(3) + m_(4) + m_(5) + m_(6))`, where m represents the masses and x represents the position.

In order to find the coordinates of the center of mass, we need to use this equation for both the x-values and the y-values.

x-values:

`x_(cm)` =
`(m_(1)x_(1) + m_(2)x_(2) + m_(3)x_(3) + m_(4)x_(4) + m_(5)x_(5) + m_(6)x_(6))/(m_(1) + m_(2) + m_(3) + m_(4) + m_(5) + m_(6))` =
`(4(-1)+6(4)+7(-3)+10(5)+2(-2)+12(3))/(4+6+7+10+2+12)` =
`((-4)+(24)+(-21)+(50)+(-4)+(36))/(41)` =
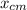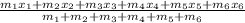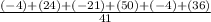`(81)/(41)` = 1.9756

y-values:

`y_(cm)` =
`(m_(1)y_(1) + m_(2)y_(2) + m_(3)y_(3) + m_(4)y_(4) + m_(5)y_(5) + m_(6)y_(6))/(m_(1) + m_(2) + m_(3) + m_(4) + m_(5) + m_(6))` =
`(4(1)+6(2)+7(-2)+10(-4)+2(4)+12(-5))/(4+6+7+10+2+12)` =
`((4)+(12)+(-14)+(-40)+(8)+(-60))/(41)` =
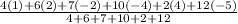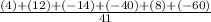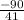`(-90)/(41)` = -2.1951

center of mass:

(1.9756, -2.1951)