Answer:
k = 3.94 (2 d.p.)
Explanation:
The given table is a grouped frequency table with continuous data (no gaps or overlaps between classes).
Mean of grouped data
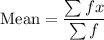
(where f is the frequency and x is the class mid-point).
To find an estimate of the mean, assume that every reading in a class takes the value of the class mid-point.
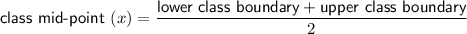
Calculate the mid-points (x) of each class and fx:

Given the mean is 4.09 kg, substitute the found values of f and fx (from the above table) into the mean formula and solve for k:
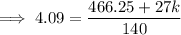
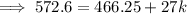
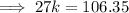
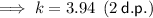
Therefore, the value of k is 3.94 (2 d.p.)