Question

asked Sep 12, 2022 205k views

1 Answer

The Mask · Answer 1 · 2022-09-18T03:30:40+0000

Given:

A figure of a parallelogram.

The vertex angles are
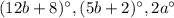$(12b+8)^\circ,(5b+2)^\circ,2a^\circ$ .

To find:

The values of a and b.

Solution:

We know that the pairs of consecutive angles of a parallelogram are supplementary angles. It mean their sum is 180 degrees.

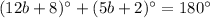$(12b+8)^\circ+(5b+2)^\circ=180^\circ$ (Supplementary angles)

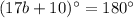
$(17b+10)^\circ=180^\circ$

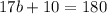
17b+10=180

Subtract 10 from both sides.

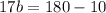
17b=180-10

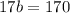
17b=170

Divide both sides by 17.

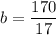
b=(170)/(17)

b=10

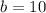
Now,

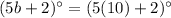
$(5b+2)^\circ=(5(10)+2)^\circ$

$(5b+2)^\circ=(50+2)^\circ$

$(5b+2)^\circ=52^\circ$

And,

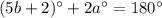$(5b+2)^\circ+2a^\circ=180^\circ$ (Supplementary angles)

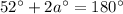
$52^\circ+2a^\circ=180^\circ$

$2a^\circ=180^\circ-52^\circ$

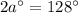
$2a^\circ=128^\circ$

Divide both sides by 2.

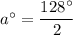
$a^\circ=(128^\circ)/(2)$

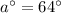
$a^\circ=64^\circ$

a=64

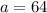
Therefore, the value of a is 64 and the value of b is 10.

Please log in or register to add a comment.