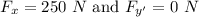Solution :
Given :
Force, F = 500 N
Let
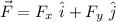
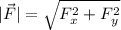
∴
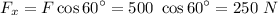
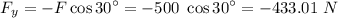 (since
(since
 direction is in negative y-axis)
direction is in negative y-axis)
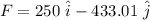
So scalar components are : 250 N and 433.01 N
vector components are :
 and
and

1. Scalar components along :
x' axis = 500 N, since the force is in this direction.
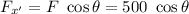
Here, θ = 0° , since force and axis in the same direction.
So, cos θ = cos 0° = 1
∴

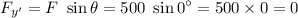
 but here θ is 90°. So the force ad axis are perpendicular to each other.
but here θ is 90°. So the force ad axis are perpendicular to each other.
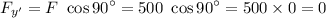
∴
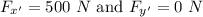
2. Scalar components of F along:
x-axis :
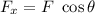 , here θ is the angle between x-axis and F = 60°.
, here θ is the angle between x-axis and F = 60°.
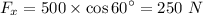
y'-axis :
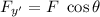 , here θ is the angle between y'-axis and F = 90°.
, here θ is the angle between y'-axis and F = 90°.
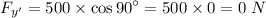
∴