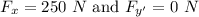Question

The 500-N force F is applied to the vertical pole as shown(1) Determine the scalar components of the force vector F along the x'- and y'-axes. (2) Determine the scalar components of F along the x- and y'-axes.

Answer 1

Given :

Force, F = 500 N

Let
`$ \vec F = F_x\ \hat i + F_y\ \hat j$`

`$|\vec F|=√(F_x^2+F_y^2)$`

∴
`$F_x=F \cos 60^\circ = 500 \ \cos 60^\circ = 250 \ N$`

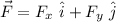
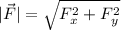
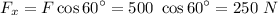
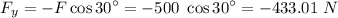`$F_y=-F \cos 30^\circ = -500 \ \cos 30^\circ = -433.01 \ N$` (since
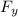`$F_y$` direction is in negative y-axis)

`$F=250 \ \hat i - 433.01 \ \hat j$`

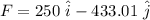
So scalar components are : 250 N and 433.01 N

vector components are :
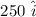`$250 \ \hat i$` and
`$-433.01\ \hat j$`

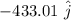
1. Scalar components along :

x' axis = 500 N, since the force is in this direction.

`$F_(x')= F \ \cos \theta = 500\ \cos \theta$`

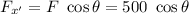
Here, θ = 0° , since force and axis in the same direction.

So, cos θ = cos 0° = 1

∴
`$F_(x')=500 * 1=500\ N$`

`$F_(y')= F \ \sin \theta = 500\ \sin 0^\circ=500 * 0=0$`

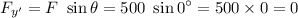
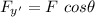`$F_(y')=F\ cos \theta$` but here θ is 90°. So the force ad axis are perpendicular to each other.

`$F_(y')=F\ \cos 90^\circ= 500 \ \cos 90^\circ = 500 * 0=0$`

∴
`$F_(x')= 500\ N \text{ and}\ F_(y')=0\ N$`

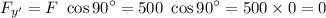
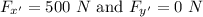
2. Scalar components of F along:

x-axis :

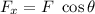`$F_x=F\ \cos \theta$`, here θ is the angle between x-axis and F = 60°.

`$F_x=500 * \cos60^\circ=250\ N$`

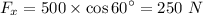
y'-axis :

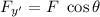`$F_(y')=F\ \cos \theta$`, here θ is the angle between y'-axis and F = 90°.

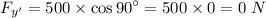
`$F_(y')=500 * \cos90^\circ=500* 0=0\ N$`

∴
`$F_(x)= 250\ N \text{ and}\ F_(y')=0\ N$`